IndieCoder's Blog | Web Development Articles & Tutorials

Minimax ‌algorithm ရဲ့ အခြေခံတွေကို ‌ရှေ့တစ်ပိုင်းမှာ လေ့လာခဲ့ပါတယ်။ ဒီအပိုင်းမှာတော့ Minimax ကို Tictactoe ဂိမ်းလေးမှာ ထည့်ပြီး အသုံးပြုမှာ ဖြစ်ပါတယ်။

Tictactoe Game

ဂိမ်းလေးထဲမှာ Algorithm အတွက် လိုအပ်တဲ့ Function တွေကို အရင်အပိုင်းမှာ ဖော်ပြခဲ့ပြီး ဖြစ်ပါတယ်။ နမူနာဂိမ်းလေးကို Tictactoe Board Module – Pastebin.com မှာ ကြည့်နိုင်ပါတယ်။ အဓိကသုံးရမယ့် Function တွေကို အောက်မှာပြထားပါတယ်။ ဒါတွေ ပါရင်ပဲ Minimax ကို သုံးလို့ရပါပြီ။ ကျွန်တော်ရေးထားတဲ့အတိုင်း အကုန်တူစရာမလိုပါဘူး။

Symbol = str
Square = int

class Board:
    def push(move):
        # Make a move for a player
    def undo(move):
        # Undo a move
    def empty_squares() -> list[Square]:
        # Give all empty squares on current board
    def is_gameover() -> bool:
        # Return whether the game is ended or not
    def winner() -> Symbol:
        # Return the winnner of the match if exists

ဒါတွေက Algorithm ထဲမှာ သုံးရမယ့် Function တွေပါ။ ဂိမ်းအတွက် လိုအပ်မယ့် တစ်ခြား Function တွေတော့ ပါဉီးမှာပါ။ ကျွန်တော်ကတော့ Pygame နဲ့ GUI ဆွဲထားပါတယ်။ GUI က တစ်ကယ်တော့ မလိုအပ်ပါဘူး။ Terminal ထဲမှာ text-based ကစားနိုင်ရင်ကို Algorithm သုံးလို့ရပါပြီ။

AI Module

အရင်ဆုံး AI class ကို တည်ဆောက်ပါမယ်။ Class ထဲမှာ ‌ရေးမယ့်ပုံစံကို အောက်မှာ ပြထားပါတယ်။

from tictactoe.board import Board

Symbol = str 
Score = int
Square = int

class AI:
    def __init__(self, ai: Symbol, foe: Symbol):
        self.ai = ai
        self.foe = foe

    def evaluate(self) -> Score:
        pass

    def minimax(self) -> tuple[Score, Square]:
        pass

    def get_best_move(self) -> Square:
        pass

အပေါ်မှာ ရေးထားတဲ့ နှစ်ကြောင်းက Parameter တွေကို ရှင်းပြရတာ လွယ်အောင် Type hint အတွက်ထည့်ထားတာပါ။ တစ်ကယ်မလိုပါဘူး။

AI class ထဲကို ကစားရမယ့် သင်္ကေတတွေကို ထည့်ပေးရပါမယ်။ Tictactoe ဂိမ်းကိုရေးပြီဆိုရင် Table ကို Data structure တစ်ခုခုနဲ့ သိမ်းထားမှာဖြစ်ပါတယ်။ ကျွန်တော့်ဂိမ်းထဲမှာဆိုရင် Tictactoe board ပေါ်ကတန်ဖိုးတွေကို List နဲ့ သိမ်းထားပါတယ်။ နမူနာတစ်ခု Terminal ထဲမှာ ရေးပြပါမယ်။

# Table Storage Example
board = Board()
board.table        
# Console Output
# ['#', '#', '#', '#', '#', '#', '#', '#', '#']

board.push(1, 'O')
board.push(4, 'X')
board.push(8, 'O')

board.table
# Console Output
# ['#', 'O', '#', '#', 'X', '#', '#', '#', 'O']

GUI မှာ ကိုယ်ကြိုက်တဲ့ ပုံနဲ့ ပြလို့ရပေမယ့် Game logic တွေလုပ်ဖို့ဆိုရင် အထဲမှာ ဒီလိုတစ်နည်းနည်းနဲ့ သိမ်းရပါတယ်။ ကျွန်တော့်ဂိမ်းထဲမှာ ဆိုရင် Player တွေကို ‘O’, ‘X’ ဆိုပြီး သတ်မှတ်ထားပါတယ်။ ဒါကြောင့် ထိပ်ဆုံးမှာ Symbol ကို String type ပြထားတာပါ။ ဒီတော့ AI ကို ‘X’ အဖြစ် ကစားမယ်ဆိုရင် AI(‘X’, ‘O’) လို့ ထည့်ပေးရပါမယ်။ ‘O’, ‘X’ မှမဟုတ်ပါဘူး။ တစ်ခြားထားချင်တဲ့ သင်္ကေတ ထားလို့ရပါတယ်။ ကိုယ့်ရဲ့ဂိမ်းထဲမှာက Player တွေကို 1, 0 လို့ထားတယ်ဆိုရင်လည်း 1, 0 ထည့်ပေးရုံပါပဲ။

Evaluating the game

Minimax algorithm ကို သုံးဖို့ဆိုရင် ဂိမ်းမှာ ဘယ်သူနိုင်နိုင်ခြေရှိလဲ တွက်ရပါမယ်။ ဒါကြောင့် evaluate-function ထဲမှာ အနိုင်၊ အရှုံးနဲ့ သရေကို Integer (Score) အဖြစ် ‌ပြောင်းပေးထားပါတယ်။ ဒါမှ နောက်ပိုင်း တွက်ရ လွယ်မှာပါ။ တန်ဖိုးတွေကတော့ ဘာဖြစ်ဖြစ် ကြိုက်ရာထားနိုင်ပါတယ်။ (e.g., 100, -100, 50) အဓိကက နိုင်ရင် (+) ရှုံးရင် (-) ဖြစ်ရပါမယ်။

def evaluate(self, board: Board) -> Score:
    if board.winner() == self.ai:  
        return 1 
    elif board.winner() == self.foe:  
        return -1 
    return 0

Minimax Tree

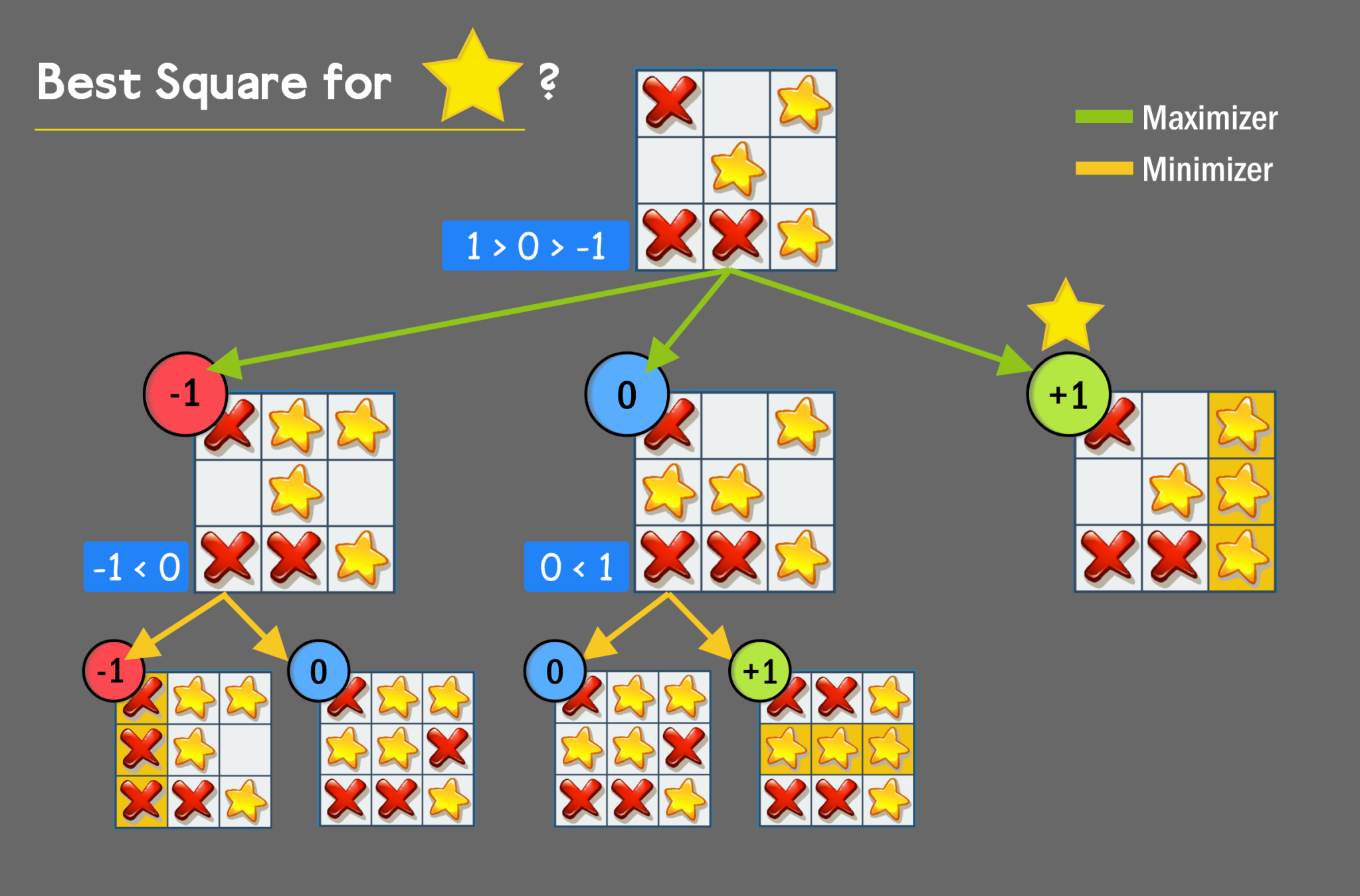
ကုဒ်မရေးခင်မှာ Minimax ရဲ့ အလုပ်လုပ်ပုံကို အရင်လေ့လာကြပါမယ်။ AI ကစားရမယ့် အလှည့်ရမှာ Minimax-function ကို ခေါ်ပြီး AI အတွက် အကောင်းဆုံးအကွက်ကို ရှာမှာ ဖြစ်ပါတယ်။ Algorithm က ပေးထားတဲ့ အဆင့်ကနေစပြီး လွတ်တဲ့ အကွက်တိုင်းကို တစ်လှည့်ပြီးတစ်လှည့် အဆုံးထိကစားကြည့်မှာပါ။ အဲဒီအထဲကမှ Win or Draw ဖြစ်စေမယ့် အကွက်ကို ရွေးထုတ်ပေးမှာပါ။ Evaluate-function ကထုတ်ပေးတဲ့ Score ကိုသုံးပြီး နောက်ဆုံးရလဒ်ကို တွက်မှာဖြစ်ပါတယ်။ ကိုယ့်အလှည့်မှာ Score ကို +1 (အများဆုံး) ရအောင်ကစားမှာ ဖြစ်လို့ AI ကို Maximizing Player လို့သတ်မှတ်ပါတယ်။ ပြိုင်ဘက်ရဲ့ ကစားကွက်ကို ခန့်မှန်းရာမှာတော့ ပြိုင်ဘက်က သူ့အတွက် နိုင်မယ့် ရလဒ်ဖြစ်တဲ့ -1 (အနည်းဆုံး) ရအောင် ကစားမယ်လို့ ယူဆပါတယ်။ ဒါကြောင့် ပြိုင်ဘက်ကို Minimizing Player လို့ ခေါ်ပါတယ်။ ဒါကို ပိုပြီး ရှင်းအောင် Tree diagram နဲ့ အောက်မှာ ပြထားပါတယ်။

Minimax က လွတ်တဲ့ အကွက်တွေကို ပွဲပြီးတဲ့ထိ ကစားကြည့်ပြီးမှ ကိုယ့်အတွက် မရှုံးနိုင်မယ့် အကွက်ကို အပေါ်ကို ပြန်ပြီး ရှာတာဖြစ်ပါတယ်။ Tree diagram မှာဆိုရင် လွတ်တဲ့ အကွက်သုံးကွက်ထဲကမှ နိုင်မယ့်အကွက်ကို ရွေးသွားတာဖြစ်ပါတယ်။ X ရဲ့ အလှည့်မှာဆိုရင် Score နည်းတာတွေကိုပဲ ‌ရွေးထားတာကို တွေ့ရမှာပါ။ သူက ပြိုင်ဘက်ကစားသမားဖြစ်လို့ ကိုယ့်အမှတ်ကို နည်းနိုင်သမျှနည်းအောင် ကစားမယ်လို့ ယူဆထားတာ ဖြစ်ပါတယ်။ ပြိုင်ဘက်က အကောင်းဆုံးကစားရင်တောင် Minimax က ဖြစ်နိုင်တဲ့ အကွက်တိုင်းကို အကုန်ကစားပြီးမှ ပြန်ရွေးတာဆိုတော့ ဘယ်တော့မှ ရှုံးမှာ မဟုတ်ပါဘူး။

Minimax Function

Minimax-function ထဲမှာ Board object ရယ်၊ ကစားရမယ့် အလှည့်ရယ် ကို Parameter အဖြစ် ယူပါမယ်။ Minimax က Recursive function ဖြစ်တဲ့ အတွက် Game over ဖြစ်ရင် Return လုပ်ပေးပါမယ်။ Return value တွေအဖြစ် Score နဲ့ ‌‌အကောင်းဆုံးအကွက် ကိုတွဲပြီး ထုတ်ပေးရပါမယ်။ Algorithm က တွက်ဖို့အတွက် Score ကိုပဲလိုတာဖြစ်ပါတယ်။ ဒါပေမယ့် ဒီ Function တစ်ခုတည်းနဲ့ အကောင်းဆုံးအကွက်ကို တန်းရနိုင်အောင် Best square ကိုပါ တွဲပြီး ထုတ်‌ပေးတာဖြစ်ပါတယ်။ ဒီပထမဆုံး Return ကတော့ Gameover ဖြစ်ပြီမလို့ Best square မလိုပါဘူး။

def minimax(self, board: Board, ai_turn: bool) -> tuple[Score, Square]:
    if board.is_gameover():
        return self.evaluate(board), None

Function ထဲမှာ အကွက်လွတ်တွေအကုန်လုံးကို တစ်ခုချင်းစီ for-loop ပတ်ပြီး အကောင်းဆုံးအကွက်တွေကို ရှာမှာ ဖြစ်ပါတယ်။ AI အလှည့်ဆိုရင် ရလာတဲ့ Score တွေထဲက အများဆုံးရတဲ့ အကွက်ကို ရွေးပါတယ်။ ပြိုင်ဘက်အလှည့်ဆိုရင်တော့ အနည်းဆုံးရတဲ့အကွက်ကို ရွေးမှာပါ။ ဒီနေရာမှာ Score အများဆုံး နှိုင်းယှဉ်ဖို့အတွက် max_eval ကို -1000 စသတ်မှတ်ထားတာကို တွေ့ရမှာပါ။ စစချင်းနှိုင်းယှဉ်မယ့် တန်ဖိုးကို တန်းပြောင်းချင်လို့ ဒီလို ထားထားတာဖြစ်ပါတယ်။ ရလာမယ့် Score တွေက -1, 0, 1 ဖြစ်တဲ့ အတွက် ပထမ Score တစ်ခုရလာတာနဲ့ max_eval က တန်းပြောင်းသွားမှာပါ။ စစချင်းတန်ဖိုးကို အရင်ဆုံး Assign လုပ်လို့ရပေမယ့် Algorithm အနေနဲ့ ရှုပ်မှာစိုးလို့ ဒီလို အစွန်းရောက်တန်ဖိုးတစ်ခု သတ်မှတ်ထားတာပါ။ သတိထားရမှာက max_eval ရဲ့ Initial တန်ဖိုးက အနည်းဆုံး Score ထက် ငယ်ရမှာဖြစ်ပါတယ်။

def minimax(self, board: Board, ai_turn: bool) -> tuple[Score, Square]:
    ...
    if ai_turn:  
        max_eval = -1000 
        best_square = None 
        # Loop through all empty squares
        for square in board.empty_squares:
            # Make a move and get evaluation
            board.push(square, self.ai)  
            eval_ = self.minimax(board, False)[0]  
            board.undo(square)
            # Compare if greater than max value or not
            max_eval = max(eval_, max_eval)  
            # If it's max value, set the square as best square
            if eval_ == max_eval:  
                best_square = square  
        return max_eval, best_square

ဒါကတော့ AI အလှည့်မှာ run ရမယ့် Maximizing algorithm ပါ။ For-loop ထဲမှာ အကွက်လွတ်တခုစီကို ထည့်ကြည့်ပြီး ရလာတဲ့ Evaluation score ကို max_eval နဲ့ နှိုင်းယှဉ်ကြည့်ပါတယ်။ Score က max_eval ထက်များနေရင် အခုထည့်ထားတဲ့ အကွက်ကို အကောင်းဆုံး အကွက်လို့ သတ်မှတ်ပါတယ်။ Evaluation ရှာတဲ့ အခါမှာ Minimax-function ကိုပဲ Recursive ခေါ်ထားပြီး ai_turn ကို False ပေးထားတာကို တွေ့ရမှာပါ။ နောက်အလှည့်ဟာ ပြိုင်ဘက်အလှည့်ဖြစ်တဲ့အတွက် အနည်းဆုံး Score ရှာရမှာ ဖြစ်လို့ Flag ပြောင်းလိုက်တာပါ။ Minimizing algorithm ကလည်း ဒီအတိုင်းပါပဲ။ Max အစား Min ပြောင်းတာရယ်၊ အကွက်ထည့်တဲ့ နေရာမှာ ပြိုင်ဘက်ရဲ့ သင်္ကေတ ထည့်ပေးရတာရယ်ပဲ ကွာပါတယ်။ Min_eval ရဲ့ initial value ကိုလည်း Positive (+) ပြောင်းပေးရပါမယ်။

def minimax(self, board: Board, ai_turn: bool) -> tuple[Score, Square]:
    ...
    else:  
        min_eval = 1000 
        best_square = None 
        for square in board.empty_squares:  
            # Make move as opponent
            board.push(square, self.foe)  
            eval_ = self.minimax(board, True)[0]  
            board.undo(square)  
            # Find minimum score
            min_eval = min(eval_, min_eval)  
            if eval_ == min_eval:  
                best_square = square  
        return min_eval, best_square

Minimax algorithm ကတော့ ဒါပါပဲ။ Function တစ်ခုလုံးကို အောက်မှာ ပြန်ပြထားပါတယ်။

def minimax(self, board: Board, ai_turn: bool) -> tuple[Score, Square]:
 
    if board.is_gameover():
        return self.evaluate(board), None
 
    if ai_turn:  
        max_eval = -1000 
        best_square = None 
        # Loop through all empty squares
        for square in board.empty_squares:
            # Make a move and get evaluation
            board.push(square, self.ai)  
            eval_ = self.minimax(board, False)[0]  
            board.undo(square)
            # Compare if greater than max value or not
            max_eval = max(eval_, max_eval)  
            # If it's max value, set the square as best square
            if eval_ == max_eval:  
                best_square = square  
        return max_eval, best_square  
 
    else:  
        min_eval = 1000 
        best_square = None 
        for square in board.empty_squares:  
            # Make move as opponent
            board.push(square, self.foe)  
            eval_ = self.minimax(board, True)[0]  
            board.undo(square)  
            # Find minimum score
            min_eval = min(eval_, min_eval)  
            if eval_ == min_eval:  
                best_square = square  
        return min_eval, best_square

ကျန်တာကတော့ Tictactoe ဂိမ်းထဲမှာ AI ထည့်ဖို့ပဲ ရှိပါတယ်။ ဒီ ‌algorithm ‌ရေးထားတာနဲ့ ပတ်သက်ပြီး နားမလည်တဲ့ အပိုင်းရှိရင်လည်း Comment/Messenger မှာ မေးမြန်းနိုင်ပါတယ်။ အတတ်နိုင်ဆုံး ပြန်ရှင်းပြပေးပါမယ်။ နောက်ဆုံး Function တစ်ခုအနေနဲ့ Minimax ကို သုံးပြီး အကောင်းဆုံးအကွက်ကို ထုတ်ပေးတဲ့ Function ကို AI class ထဲမှာ ရေးပါမယ်။

def get_best_move(self, board: Board) -> Square:  
    score, best_move = self.minimax(board, True)
    # Max score AI will get
    print(score)  
    return best_move

AI Player

Tictactoe ဂိမ်းကို Run မယ့် main.py ထဲမှာ AI player ကို ထည့်မှာဖြစ်ပါတယ်။ အရင်အပိုင်းမှာဖော်ပြခဲ့တဲ့ နမူနာ Program လေးကို ပြန်ပြပေးပါမယ်။

from tictactoe.board import Board
from tictactoe.gui import Gui
 
import pygame
 
def main():
    board = Board()
    player = board.P1
    ai_player = board.P2
 
    gui = Gui(board, "Tic-tac-toe AI: The Unbeatable")
 
    clock = pygame.time.Clock()
    running = True
    while running:
        gui.update_display()
        clock.tick(60)
 
        for event in pygame.event.get():
            if event.type == pygame.QUIT:
                running = False
            if event.type == pygame.MOUSEBUTTONUP:
                if board.is_gameover():
                    board.reset()
                    continue
 
                square = gui.get_clicked_tile(event.pos)
                if square is not None:
                    board.move(square)
    pygame.quit()

အရင်ဆုံး AI ကို Initialize လုပ်ပါမယ်။

# Import AI
from engine import AI
from tictactoe.board import Board
from tictactoe.gui import Gui
 
import pygame
 
def main():
    board = Board()
    player = board.P1
    ai_player = board.P2
    # Initialize the ai 
    ai = AI(ai_player, player)
 
    gui = Gui(board, "Tic-tac-toe AI: The Unbeatable")
    ...

ပြီးရင် Game loop ထဲမှာ AI အလှည့်ရောက်တဲ့ အခါ အကောင်းဆုံးအကွက်ကို ရှာပေးမှာဖြစ်ပါတယ်။

...
while running:  
    gui.update_display()  
    clock.tick(60)  
 
    if not board.is_gameover() and board.turn == ai_player:  
        ai_move = ai.get_best_move(board)  
        board.move(ai_move)
 
    ...

ဒီလို Main program ထဲကို AI ထည့်တာက ကိုယ်ရေးထားတဲ့ ဂိမ်း‌ပုံစံပေါ်မူတည်ပြီး သုံးရမှာပါ။ အပေါ်က နမူနာ အဖြစ်ပြထားတာပါ။ ကျွန်တော်တင်ပေးထားတဲ့ Board module ပုံစံအတိုင်းရေးထားရင်တော့ ဒီအတိုင်း တန်းသုံးလို့ရပါတယ်။ ဒီအဆင့်မှာ ဆိုရင်တော့ Tictactoe AI လေးကို ဖန်တီးလို့ ပြီးသွားပါပြီ။ Project တစ်ခုလုံးကို Github မှာ တင်ပေးထားတာပါတယ်။

Project Link–> IndieCoderMM/tictactoe-ai

Conclusion

ဒီ Project လေးကို လိုက်လုပ်ရင်း Minimax Algorithm အကြောင်းကို သေသေချာချာ နားလည်လာပြီး ကိုယ်ပိုင် Project တွေမှာ အသုံးချနိုင်မယ်လို့ မျှော်လင့်ပါတယ်။ Minimax algorithm က တစ်ခြားအဆင့်မြင့်ဂိမ်းတွေဖြစ်တဲ့ Checker, Connect-4, Chess စတာတွေမှာလဲ ကောင်းကောင်းအလုပ်လုပ်နိုင်ပါတယ်။ ဒီလိုဂိမ်းတွေမှာ Minimax အသုံးပြုပုံကို နောက် Project တွေမှာ ဆက်ပြီး တင်ပေးပါမယ်။

Happy Coding!